《机器学习》 第十章 降维与度量学习
第十章 降维与度量学习
10.1 k近邻学习(KNN)
核心思想:对于测试样本,基于距离度量来找出训练集中与其最近的几个样本,然后根据邻居信息来预测,一般使用投票法(分类)或者平均法(回归),也可加权(根据距离)。
懒惰学习的杰出代表,仅仅只是保存训练样本,没有显式地训练。
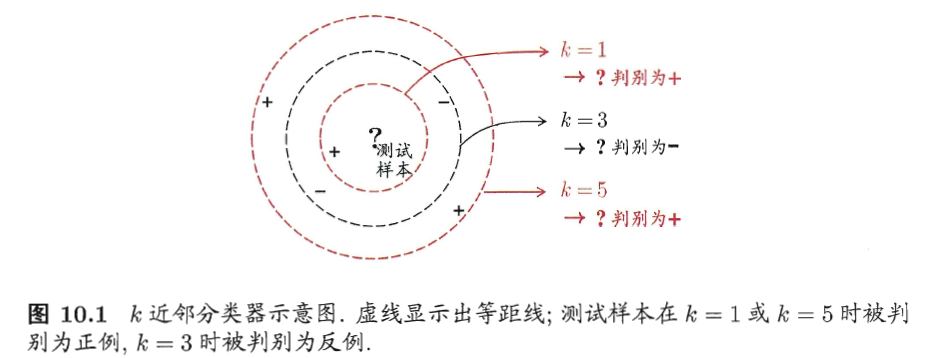
理论上,虽然KNN简单,但是性能上的泛化错误率不会超过贝叶斯最优分类器的两倍。
10.2 低维嵌入【略】
10.3 主成分分析(PCA)
主成分分析主要用于降维,还可用于去噪。对于降维,可以理解为这么一个问题:如何用超平面对所有样本进行恰当的表达?具有以下性质:
- 最近重构性:样本点到超平面的距离都足够近
- 最大可分性:样本点到超平面上的投影都尽量分开
考虑这两个性质,都可以推导出相同的结果。
最近重构性【略】
最大可分性
样本点x到新空间中投影为$W^Tx$,如果要使样本点尽量分开,则样本点的方差应该最大化。
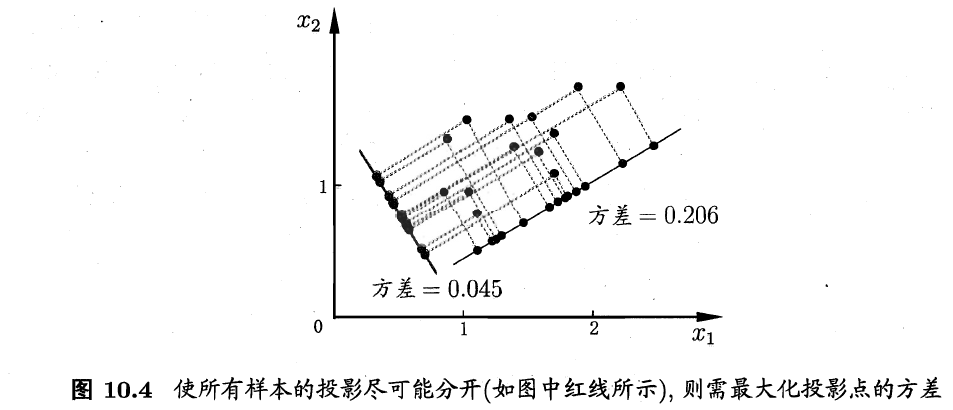
协方差矩阵为:
优化目标可改写为:
使用拉格朗日乘子法:
也就是求解左边的特征值。
具体来说:求解特征值,然后按照特征值的大小进行排序,选取前d个特征值即可。

10.4 核化线性降维【略】
评论
