《机器学习》 第八章 集成学习
第八章 集成学习
8.1 个体与集成
集成学习就是构建并结合多个学习器来完成学习任务,也被称作是多分类器系统。
一般是先产生一组“个体学习器”,再根据某种策略将它们结合起来,一般由现有的算法生成,比如决策树、神经网络等等;既有同质的集成也有异质的集成,取决于是否使用相同的基学习算法。
集成学习将多个学习器进行结合,常常可以获得比单一学习器更优秀的性能。这对于弱学习器更加明显。
通常来说,将好坏的东西混合在一起,会比最好的差一些,最差的好一些,平均了。
但是我们想要的是比最好的还好一些。
集成学习的原则是要:好而不同。既要有一定的准确性,还要有多样性,学习器之间有差异。但是这两样又是互相冲突的。
分类:
1、强依赖关系、必须串行化生成的序列化方法:如Boosting
2、并行化,如:Bagging和RF
8.2 Boosting【有省略】
工作机制:先用训练数据生成一个基学习器,再根据基学习器的表现对训练样本进行调整,使得做错的样本收到更多的关注,调整以后再训练下一个基分类器。
代表算法是AdaBoost【只能用于二分类】
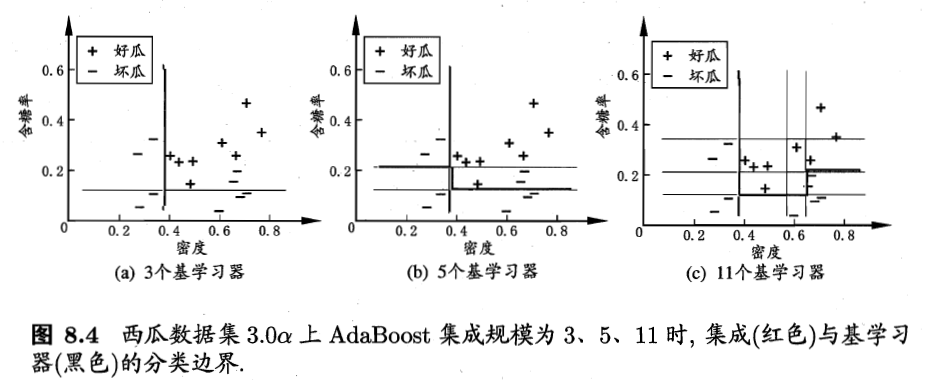
从偏差-方差角度理解,Boosting算法主要是为了降低偏差,因此可以从泛化性能弱的学习器中构建很强的集成。如上图。
8.3 Bagging和随机森林
想要得到比较强的集成,个体学习器应该要互相独立;但是现实任务独立无法做到,但是可以设法实现数据集有较大的差异。如进行采样【前面讲得自助采样法】,每个子集训练一个学习器;这个子集不能太小,不然无法学习足够好。
8.3.1 Bagging
基于自助采样法,抽取一个样本再放回去继续抽,这样m个样本抽取m次,大约有0.632的样本出现在训练集。
因此可以构造T个学习器,然后对预测输出进行结合,比如分类使用简单投票法、回归任务使用平均法,票数相同时可以使用随机也可以使用置信度。
包外估计有许多优点。可以用来做验证集、辅助剪枝等等
从偏差-方差角度看,Bagging主要关注降低方差
8.3.2 随机森林
是以决策树为基学习器构建Bagging集成的基础上,进一步在决策树的训练过程中引入了随机属性选择。
传统的决策树在选择划分属性时选择最优属性,在RF中,先随机选择一个包含k个属性的子集,再选择最优属性。k对于1时,随机选择一个属性;推荐k=log2 维度。
随机森林简单、容易实现、计算开销小。
8.4 结合策略
结合学习器的好处:
- 假设空间比较大,单个学习器可能再训练集不错,但是泛化性能可能不佳,结合多个学习器可以减少这一风险
- 算法可能陷入局部最小,多次运行结合可能可以跳出局部最小。
1、平均法【数值型输出】
- 简单平均法
- 加权平均法
一般而言,个体性能差距较大,可以使用加权平均法;个体性能相近使用简单平均法
2、投票法【类别】
- 绝对多数投票法:过半,否则拒绝
- 相对多数:票数最多的
- 加权投票法
3、学习法:通过另一个学习器来结合
- 多响应线性回归
- 贝叶斯模型平均
