《机器学习》 第六章 支持向量机

第六章 支持向量机

在这一节中，将介绍SVM的基本思想，以及转换成数学表达式。

6.1 间隔与支持向量

SVM的直观理解

对于一个二分类问题，我们基于一个训练集D可以在样本空间（特征空间）中找到一个超平面来区分开，但是超平面可能很多，我们应该找哪一个呢？

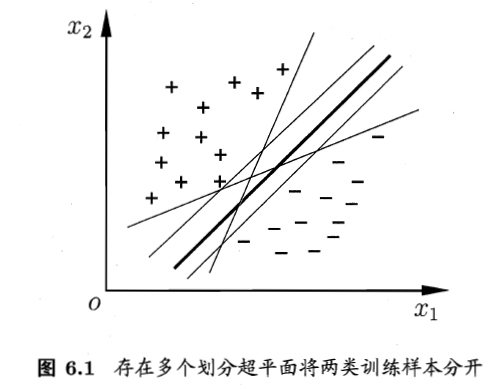
直观上来说，我们喜欢中间粗的线，因为最能够将两类样本分开，而且鲁棒性最高，抗干扰。

---

基本表示

在样本（特征）空间中，划分超平面可以通过如下方程描述：

$$\begin{align} w^T x + b = 0 \end{align}$$

空间中点到超平面的距离可以为：

$$\begin{align} r = \frac {| w^T x + b|}{|| w||} \end{align}$$

对于两类样本，正类和反类应该满足：（在曲线两侧）

$$\begin{align} { w^T x_i + b} \geq 0, y_i & = +1 \\ { w^T x_i + b} \leq 0, y_i & = -1 \end{align}$$

支持向量

距离超平面最近的几个训练样本使得上式成立，他们就被称作是支持向量【虚线上圈出来的点】。

间隔（margin）

而一对异类的支持向量到超平面的距离，就是间隔：

$$\begin{align} margin=2r = 2 \cdot \frac {| w^T x + b|}{|| w||} \end{align}$$

---

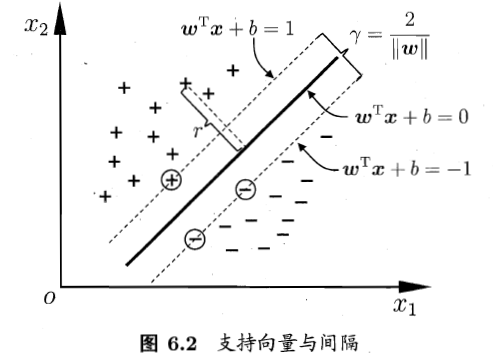
SVM的数学表示

而支持向量机核心思想就是最大间隔的分类器，在满足分类的情况下使间隔最大化。

我们可以对公式3、4【约束条件】简化：代入y

$$\begin{align} s.t. \quad y_i ({ w^T x_i + b}) \geq 0 \end{align}$$

又因为左式必定能找到一个下界R，即：

$$\begin{align} \exist \ R > 0, \ \min \ y_i ({ w^T x_i + b}) = R \end{align}$$

因为在坐标系中对直线参数统一放缩之后，表示的仍然是同一条直线，公式6可以转为：

$$\begin{align} s.t. \quad y_i ({ w^T x_i + b}) \geq 1 \end{align}$$

我们还可以对公式5化简。因为分子部分大于0，且必定存在一个下界，又因为在坐标系中对直线参数统一放缩之后，表示的仍然是同一条直线，所以，对于分子部分，我们也可以用1来替换，即：

$$\begin{align} \max_{w,b} \quad \frac {1}{|| w||} \end{align}$$

最优化问题常常用求最小表示，公式9又可改为

$$\begin{align} \min_{w,b} \quad \frac 1 2 {|| w||}^2 \end{align}$$

综上，SVM的基本数学模型为：

$$\begin{align} \min_{w,b} & \quad \frac 1 2 {|| w||}^2 \\ s.t. & \quad y_i ({ w^T x_i + b}) \geq 1, \ i=1,2...,m \end{align}$$

6.2 对偶问题

我们希望求解【公式11】来得到超平面的模型，w和b是模型参数，其本身是一个凸优化问题，可以使用现成的优化计算包解决，但是我们有更高效的方法。

6.2.1 拉格朗日乘子法

实质：将一个有n 个变量与k 个约束条件的最优化问题转换为一个有n + k个变量的方程组的极值问题，其变量不受任何约束。

对于有约束问题：

$$\begin{align} \max_{x,y} &\quad f(x,y) \\ s.t. & \quad g(x,y)=0 \end{align}$$

构造：

$$\begin{align} L(x,y,\lambda)=f(x,y)-\lambda \cdot g(x,y) \end{align}$$

对各个参数求偏导等于0，求解方程组即可。

6.2.2 对偶问题

对于【公式11】，我们可以使用拉格朗日乘子法得到其“对偶问题”。

对于【公式12】中的每一个约束我们添加一个拉格朗日乘子（大于0），则该问题的拉格朗日函数为：

$$\begin{align} & L( w,b, \lambda)=\frac 1 2 {|| w||}^2 + \sum_{i=1}^m{\lambda _i \cdot(1-y_i( w^T x_i+b))} \end{align}$$

则原问题的无约束表示为【先求最大再求最小】：

$$\left \{ \begin{align} &\min_{w,b} \max_\lambda L( w,b, \lambda) \quad \quad \quad \quad \quad \\ & s.t. \quad \lambda _i \geq 0 \end{align} \right.$$

那么对偶问题为：【最大最小调换顺序】【同解：原本19式的解强于17式的解，是弱对偶关系；但是由于原问题是凸二次优化问题，所以是强对偶关系，同解。】

$$\left \{ \begin{align} & \max_\lambda \min_{w,b} L( w,b, \lambda) \quad \quad \quad \quad \quad \\ & s.t. \quad \lambda _i \geq 0 \end{align} \right.$$

步骤1：求解w，b为变量时的最小值，对【公式16】中的w和b求偏导等于0得：（这一步比较简单哦）

$$\begin{align} w &= \sum_{i=1}^m {\lambda_iy_ix_i} \\ 0 &= \sum_{i=1}^m{\lambda_i y_i} \end{align}$$

把w和b代入L中消去【这里代入导数为0的值，其实就是把求最小过程中的最优解得到，再代入】，得：

$$\left \{ \begin{align} \max_\lambda \ L( \lambda) &= \frac 1 2 (\sum_{i=1}^m {\lambda_iy_ix_i})^T(\sum_{j=1}^m {\lambda_jy_jx_j}) + \sum_{i=1}^m{[\lambda _i -\lambda _i y_i( w^T x_i+b)]} \quad \quad \quad \quad \quad\\ &= \frac 1 2 \sum_{i=1}^m \sum_{j=1}^m \lambda_i \lambda_j y_i y_j x_i^T x_j + \sum_{i=1}^m \lambda _i \\ s.t. \quad & \sum_{i=1}^m{\lambda_i y_i} =0,\ \lambda_i \geq 0 \end{align} \right.$$

【如何求解$\lambda$？SMO算法】

SMO算法

对于求解公式23，可以使用通用的二次规划问题来求解，但是问题的规模正比于样本数，会有很大的开销。因此提出了很多高效算法，SMO是其中一种。

基本思路：对于m个要求解的参数，选取一对需要更新的参数，固定其他的参数。

求解出$\lambda$之后，再求出w和b即可得到模型。w可通过【公式21】求出；

$$\begin{align} \color{red} w^* &= \sum_{i=1}^m {\lambda_iy_ix_i} \end{align}$$

如何求解b？我们必定能找到一个样本使得【公式33】等式成立，实际上也就是支持向量[Xk, Yk]使之成立。样本值代入即可求得：

$$\begin{align} \color{red}{b^*} &= y_k - w^* x_k \end{align}$$

从中我们可以看出w是对样本的线性组合，而且只和虚线上的样本【支持向量】有关（因为不是支持向量的点求出的$\lambda$等于0）。
而对于b，只需要使用一个支持向量即可求解；而在实际中我们会选择更鲁棒的做法：使用所有支持向量求解的均值。

最后模型为：

$$\color{red}\begin{align} f(x) &= w^T x+b \\ &= \sum_{i=1}^m \lambda_i y_i x_i^T x_i + b^* \end{align}$$

KKT条件

将原问题【公式17】转换成对偶问题【公式19】的时候说过他们是强对偶关系【同解】。为什么呢？因为他们满足KKT条件。

$$\left \{ \begin{align} &\frac {\partial L}{\partial w} =0, \ \frac {\partial L}{\partial b} =0,\ \frac {\partial L}{\partial \lambda} =0 \\ &\lambda_i(1-y_i( w^Tx_i+b)) = 0 \\ & \lambda_i \geq 0 \\ &1-y_i( w^Tx_i+b) \leq 0 \end{align} \right.$$

【公式30】：梯度条件

【公式31.32】：互补松弛条件。当29等于0时，30或31必有一项为0。

【公式33】：可行条件

再看这张图，对于实线延伸出来的两条虚线

• 如果样本点在虚线上，那么【公式33】的值为0，则对$\lambda$的值没有约束；
• 如果不在虚线上，那么【公式33】的值不为0，则$\lambda$必须为0；

这样的话，除了线上的点有意义，其他的点都没有意义（因为等于0，【公式29】求w*时对其他样本的线性组合时自然等于0，没有作用），可以不需要这些样本。最终模型只与支持向量有关。

6.3 核函数

之前的样例较为简单，在低维空间中就线性可分。倘若线性不可分时，我们可以将样本映射到高维空间中，就变得线性可分了，如下所示

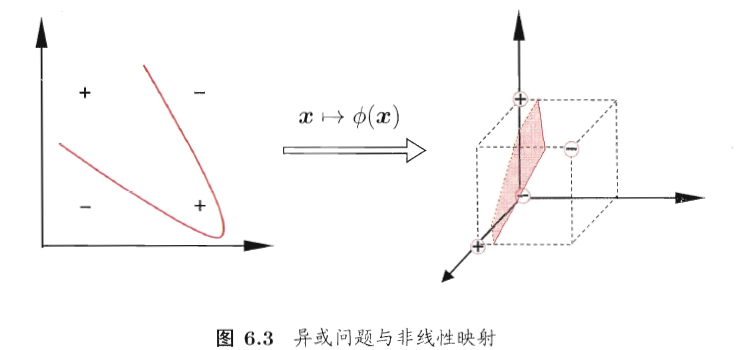
在新特征空间中划分超平面的模型为：

$$\begin{align} f( x) &= w^T \cdot {\phi( x)}+b \\ \end{align}$$

对偶问题也变成了：

$$\left \{ \begin{align} \max_\lambda \ & L( \lambda) = \frac 1 2 \sum_{i=1}^m \sum_{j=1}^m \lambda_i \lambda_j y_i y_j \phi( x_i)^T\phi( x_j) + \sum_{i=1}^m \lambda _i \quad \quad \quad \quad \quad \\ s.t. \quad & \sum_{i=1}^m{\lambda_i y_i} =0,\ \lambda_i \geq 0 \end{align} \right.$$

这里有个问题，需要求解映射后的特征空间的向量内积，可能维度很高或者是无穷维，而为了避开这个问题，我们设计了一个核函数

$$\begin{align} K(x_i,x_j)=<\phi(x_i),\phi(x_j)>=\phi(x_i)^T\phi(x_j) \end{align}$$

对偶问题进一步表示为：

$$\left \{ \begin{align} \max_\lambda \ & L( \lambda) = \frac 1 2 \sum_{i=1}^m \sum_{j=1}^m \lambda_i \lambda_j y_i y_j {\color{red}K( x_i, x_j)}+ \sum_{i=1}^m \lambda _i \quad \quad \quad \quad \quad \\ s.t. \quad & \sum_{i=1}^m{\lambda_i y_i} =0,\ \lambda_i \geq 0 \end{align} \right.$$

原本的计算过程：样本特征经过映射后的新空间中的向量表示，再计算两个向量之间的内积
引入核函数之后：直接得到内积，不需要经过映射。

$$\begin{align} f(x) &= w^T x+b \\ &= \sum_{i=1}^m \lambda_i y_i {\color{red}K( x_i, x_j)} + b^* \end{align}$$

问题：如何找到这么一个核函数？

已知映射，我们可以找到核函数；如果映射未知呢？核函数是否存在？

定理6.1：对于任意数据D={x1,x2,……,xn}，只要核矩阵是半正定的，总能找到一个与之对应的映射。

问题：新特征空间对性能的影响

选择不同的核函数就选择了不同的新特征空间，因此核函数的选择变成了最大的变量。核函数选择的不加，性能可能变得不好。常用的核函数：（高斯核也叫rbf核）

核函数还可以通过上述核的线性组合得到。

6.4 软间隔和正则化

6.4.1 软间隔

前面讨论的样本是线性可分的，然后现实中可能很多样本是线性不可分的，或者就算找到了一个线性可分的分界面，又如何确定是否过拟合呢？

缓解这个问题的方法是，允许向量机在一些样本上出错。具体来说是前面介绍的内容要求所有样本都分类正确，而软间隔允许某些样本不满足【公式8】。

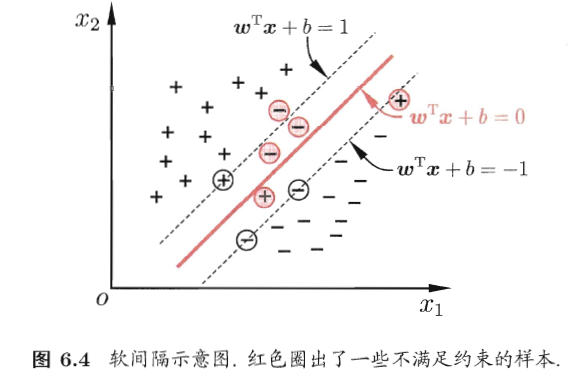
优化目标为：【这个公式是如何来的？】

$$\begin{align} \min_{w,b} \quad \frac 1 2 {|| w||}^2 + C\sum_{i=1}^m{l_{0/1}(1-y_i( w^T x_i+b))} \end{align}$$

当C无穷大时，迫使所有样本满足约束；当C的值有限时，允许一些样本不满足约束，如上图的红色样本。

$l_{0/1}$是“0/1损失函数”。因为该函数不连续，可换为其他函数：

$$\left \{ \begin{align} &hinge损失=\max(0,1-z) \quad\quad\quad\quad\quad\\ &指数损失=\exp(-z) \\ &对率损失=\log(1+\exp(-z)) \end{align} \right.$$

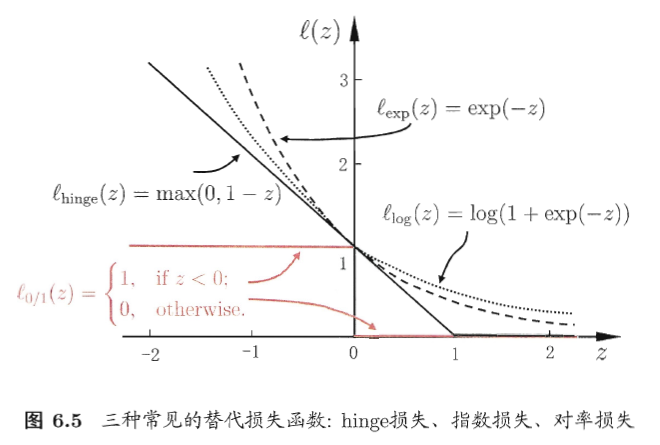
以hinge损失为例，目标转为：

$$\begin{align} \min_{w,b} \quad \frac 1 2 {|| w||}^2 + C\sum_{i=1}^m{\max(0,1-y_i( w^T x_i+b))} \end{align}$$

引入松弛变量。下面就是常用的软间隔支持向量机：

$$\left \{ \begin{align} \min_{w,b,\xi_i} \quad &\frac 1 2 {|| w||}^2 + {\color{red}C\sum_{i=1}^m \xi_i} \quad\quad\quad\quad\quad\\ s.t. \quad &y_i ({ w^T x_i + b}) \geq 1-\xi \\ &\xi \geq 0, \ i=1,2...,m \end{align} \right.$$

其对偶问题为：（差别在于对偶变量的约束不同）【可以使用与前面相同的方法求解】【当然KKT条件也略有不同】

$$\left \{ \begin{align} \max_\lambda \quad & L( \lambda) = \frac 1 2 \sum_{i=1}^m \sum_{j=1}^m \lambda_i \lambda_j y_i y_j x_i^T x_j + \sum_{i=1}^m \lambda _i \quad \quad \quad \quad \quad \\ s.t. \quad & \sum_{i=1}^m{\lambda_i y_i} =0,\\ &{\color{red}0 \leq \lambda_i \leq C},\ i=1,2...,m \end{align} \right.$$

6.4.2 正则化

通过观察上述正常形式、引入核函数、软间隔的支持向量机可以表示为下面的形式：

$$\begin{align} \min_{w,b} \quad \Omega (f) + C\sum_{i=1}^m{loss(f( x_i),y_i)} \end{align}$$

• 前面一项可以看作是描述超平面间隔的大小，称为“结构风险”，用于描述模型的某些性质（比如复杂度小，换个角度，也就是正则化问题）。也可以叫做正则化项
• 后一项表示为在训练集上的误差，称为“经验风险”，用于描述模型与训练数据的契合程度。
• 参数C对二者进行折中。看作是正则化常数

6.5 支持向量回归

这一部分内容有省略步骤

对于回归问题，传统的回归模型通过模型输出与真实输出之间的差别来计算损失。但两者完全相同时，损失为0.

而支持向量回归不同，它能够容忍一定程度的错误样本，即差别大于一定值时才计算损失。假设我们能容忍$\varepsilon$的偏差，就相当于以f(x)为中心延伸了$2\varepsilon$的区域，只要在这个范围内都认为是正确的。

如下图所示，在隔离带内的样本损失为0.

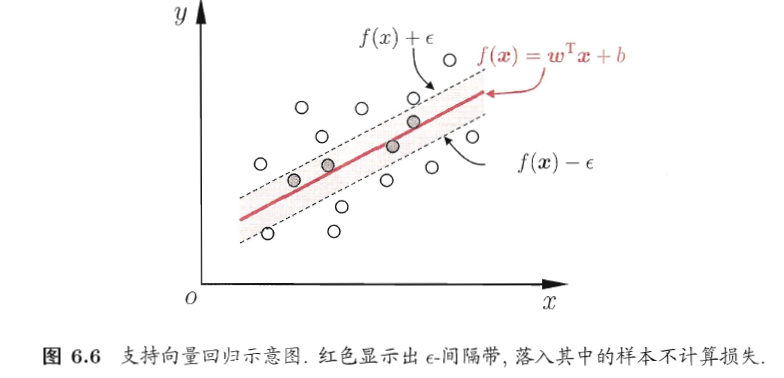
因此，SVR可以形式化为：

$$\begin{align} \min_{w,b} \quad \frac 1 2 {|| w||}^2 + C\sum_{i=1}^m{l_\varepsilon(1-y_i( w^T x_i+b))} \end{align}$$

其中，

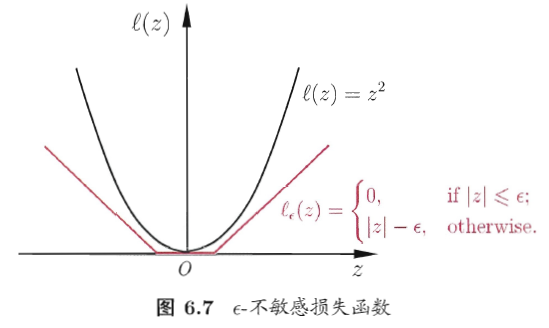
引入松弛变量，可以重写为：

$$\left \{ \begin{align} \min_{w,b,\xi_i} \quad &\frac 1 2 {|| w||}^2 + C\sum_{i=1}^m (\xi_i+ \hat{\xi_i}) \quad\quad\quad\quad\quad\\ s.t. \quad & f(x_i)-y_i \leq \varepsilon+\xi_i \\ &y_i-f(x_i) \leq \varepsilon+\hat{\xi_i} \\ &\xi_i \geq 0,\hat{\xi_i} \geq 0, \ i=1,2...,m \end{align} \right.$$

仍然是引入拉格朗日乘子，求解步骤【略】

KKT条件【略】

解得：（也可引入核函数）

$$\begin{align} f(x) &=\sum_{i=1}^m {\color{red}(\hat \lambda_i-\lambda_i)} x_i^T x_i + b^* \end{align}$$

6.6 核方法

无论SVM还是SVR，学得的模型总是能够表示成为核函数的线性组合。因此

• 表示定理：优化问题的最优解h(x)都可以表示成为核函数的线性组合。

人们发展出的一系列基于“核函数”的方法统称为“核方法”。如，通过“核化”将线性学习器变成非线性学习器。如KLDA。