《机器学习》 第五章 神经网络

第五章 神经网络

watermelon

5.1 神经元模型

5.1.1 什么是神经网络？

神经网络是具有适应性的简简单单的单元（神经元）互连的网络，能够模拟生物神经网络系统对真实世界的物体做出交互反应。

5.1.2 神经元

在生物神经网络中，当某个神经元的电位超过了一个阈值，那么他就会被激活，即“兴奋”；向其他神经元发送神经递质，进而影响其他神经元。

1943年，McCulloch和Pitts将上述情形抽象成为“M-P神经元模型”，如下图所示：

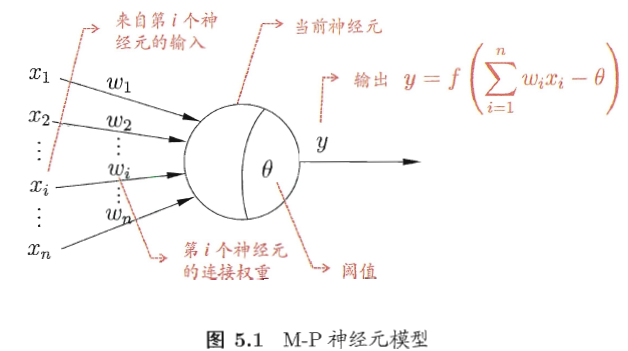
神经元接收其他n个神经元传递过来的输入信号，将这些信号通过带权重的连接进行传递，将总输入值与阈值进行比较，最后通过激活函数处理产生神经元的输出。

理想中的激活函数应该是阶跃函数，但是不光滑、不连续，实际上我们常用Sigmod函数。

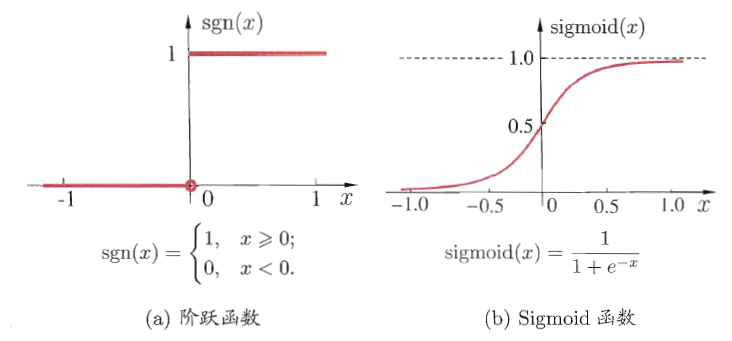
将这样的神经元按照一定的层次连接起来，就得到了神经网络。

5.2 感知机与多层网络

5.2.1 感知机

感知机由两层神经网络组成，输入层接收输入信号后传递给输出层（这里只有输出层的神经元是在运算，因此也被称作是功能神经元），输出层是M-P神经元。

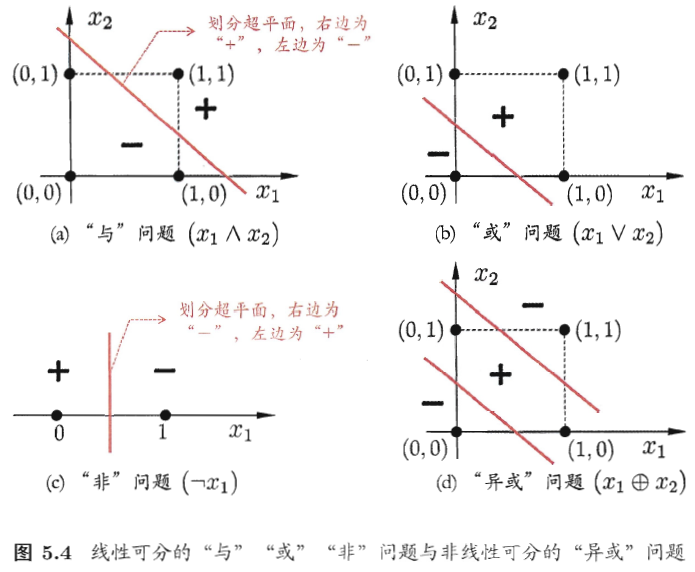
感知机能够容易的实现逻辑与或非等线性可分的问题，但是不能实现异或这样简单的非线性可分的问题。

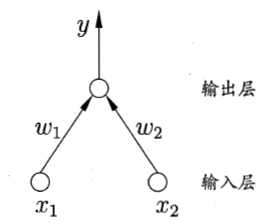
如果预测正确，则感知机不变化；否则将更新权，感知机的权重更新公式：

$$\begin{align} w_i &\gets w_i + \Delta w_i \\ \Delta w_i &= \eta(y-y_i)x_i \end{align}$$

$\eta \in (0,1)$称之为学习率。

要解决非线性可分的问题，需要在增加一层神经元，通常被称作是隐藏层。隐藏层和输出层都是有激活功能的功能神经元。

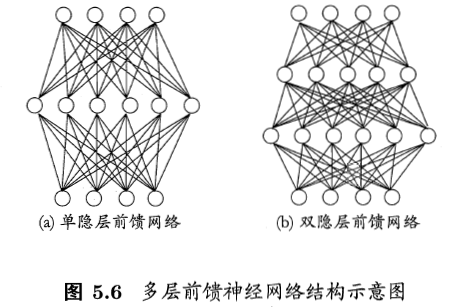
通常，神经元在同层之间不存在连接，也不存在跨层连接，这样的网络称之为“多层前馈神经网络”。

通常，输入层只接收外界输入，隐藏层和输出层对数据进行加工。通常被称作是“两层神经网络”，为了避免歧义，也叫作“单隐层网络”。

学习的过程就是根据训练数据来调整神经元之间的连接权重和每个功能神经元的阈值。换言之，神经网络学习到的东西就蕴含在权值和阈值中间。

5.3 误差反向传播算法（BP算法）

5.3.1 前向传播

层数标记：输入层记为第0层，中间层为l层，最后一层为L层，记在右上角。

前一层的输入（输入x或中间层的激活值a），

$$\begin{align} 线性组合：Z^l &= W^l \alpha^{l-1}+b^l \\ 激活：\alpha^l &= \sigma (z^l) \\ 损失函数：C &= {\frac 1 2} {||y - \alpha^L ||}_2 \end{align}$$

具体到中间的某一个节点：

$$\begin{align} 线性组合：Z^l_j &= \sum_k W^l_j \alpha^{l-1}_k+b^l_j \\ 激活：\alpha^l_j &= \sigma (z^l_j) \\ 损失函数：C &= \frac 1 2 \sum_j {(y_j - \alpha^L_j)^2} \end{align}$$

5.3.2 反向传播

四个公式：

$$\color{red} \begin{align} &BP1：\delta^L = \nabla_\alpha C \odot \sigma'(Z^L) \\ &BP2：\delta^l = ((W^{l+1})^T \cdot \delta^{l+1}) \odot \sigma'(Z^l) \\ &BP3：\frac {\partial C} {\partial w_{jk}^l} = \alpha_k^{l-1} \delta_j^l \\ &BP4: \frac {\partial C} {\partial b_{j}^l} = \delta_j^l \end{align}$$

矩阵论知识：如果$Y=W \cdot X + B,Y= \sigma(X)$，那么：

$$\begin{align} \frac {\partial C} {\partial X} &= W^T \odot \sigma'(X)\\ \frac {\partial C} {\partial X} &= W^T \cdot \frac {\partial C} {\partial Y} \\ \frac {\partial C} {\partial W} &= \frac {\partial C} {\partial Y} \cdot X^T \\ \frac {\partial C} {\partial B} &= \frac {\partial C} {\partial Y} \end{align}$$

BP1：

作为一个记号【非常有用】，表示损失值到最后一层L（从第一层隐藏层开始记数1，输入是第0层）的线性加权的输出Z的导数。

具体来说：根据链式求导法则：C先对激活后的值a求导，再点乘激活值a对加权值Z的导数。

（为什么用点乘？【公式13】因为得到加权值后，再计算激活值，这里面是n对的一对一的实数值的映射，不需要矩阵乘法）

BP2：

作为一个记号，表示损失值到第l层的线性加权的输出Z的导数。

具体来说：这是一个递推公式，假设我们已经得到了第l+1层的导数，我们要计算再到第l层的导数。先看前半部分，根据公式3（线性组合），第l+1层的Z对第l层的a的导数为$W^{l+1}$，用矩阵来描述就是矩阵$W^{l+1}$的转置左乘【公式14】我们已经得到的$\delta^{l+1}$。

接下来继续按照链式求导法则，点乘对第l层Z的导数即可。

BP3：

损失到第l层权重矩阵的第j行k列的导数：

具体来说（用记号简化公式）：

$$\begin{align} \frac {\partial C} {\partial w_{jk}^l} &= \frac {\partial C} {\partial Z_j^l} \cdot \frac {\partial Z_j^l} {\partial w_{jk}^l} \\ &= {\color{red}\delta_j^l} \cdot \frac{\partial (w_{jk}^l \alpha_k^{l-1}+b_j^l)}{\partial w_{jk}^l} \\ &= {\color{red}\delta_j^l} \cdot \alpha_j^{l-1} \end{align}$$

BP4：

损失到第l层偏置向量的第j个元素的导数：

$$\begin{align} \frac {\partial C} {\partial b_j^l} &= \frac {\partial C} {\partial Z_j^l} \cdot \frac {\partial Z_j^l} {\partial b_j^l} \\ &= {\color{red}\delta_j^l} \cdot \frac{\partial (w_{jk}^l \alpha_k^{l-1}+b_j^l)}{\partial w_{jk}^l} \\ &= {\color{red}\delta_j^l} \cdot 1 \end{align}$$

5.3.3 更新

得到了导数/梯度我们就可以方便地使用梯度更新公式更新参数，即：$\eta$ 为学习率

$$\begin{align} W^l &= W^l-\eta \cdot dW^l \\ b^l &= b^l-\eta \cdot db^l \end{align}$$

5.3.4 批量梯度下降

上述内容是针对单个样本的梯度下降，会存在：参数更新频繁，对不同样例进行更新可能会抵消效果，因此累计/批量梯度下降针对整个训练集或者一部分进行更新，频率低很多，在下降一定程度之后，进一步下降会比较慢，会获得比较好的解，尤其在训练集很大的时候。

5.3.5 过拟合

神经网络常常会过拟合。如何应对过拟合？

1、早停：训练集误差降低但是验证集升高，停止训练。

2、正则化：约束大小，降低神经网络拟合能力。

5.4 全局最小和局部最小

根据梯度下降法，如果参数空间中有多个极小值，优化的参数值就有可能落入极小值中

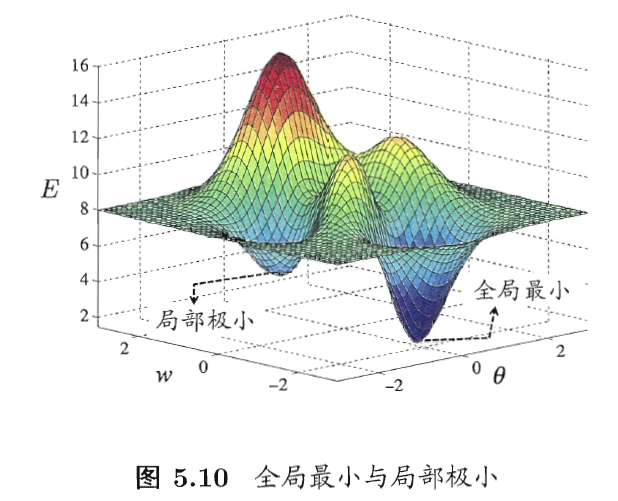
解决方法：

• 多组初始化参数值，即从不同起点开始寻找最小值
• 模拟退火算法：可以接受一定的比当前结果更差的值（次优解）
• 随机梯度下降。计算的梯度不可能为0
• 遗传算法

5.5 其他常见神经网络

有RBF、ART、SOM、级联相关网络、Elman网络、Boltzmann机。

不详细介绍。

5.6 深度学习

参数越多的模型复杂度也越高，能够完成复杂度更高的任务，但是训练效率也低、容易过拟合。但是由于计算能力、数据量的大幅提升，使得深度学习变得火热。

典型的深度学习就是很深层的网络：

• 1、增加层数
• 2、单纯增加隐藏层神经元数目

这两种方法一个是横向一个是纵向。增加层数比增加神经元数目更有效。但是深层网络不容易收敛。

难以训练的问题可以通过“预训练+微调”的方式解决，如DBN。还可以通过权值共享解决，如CNN。

对深度学习的理解：

通过多层处理，可以将低层次的特征表示为高层次的特征，然后就可以用简单模型完成复杂的分类任务。可以理解为“提特征”、“特征学习”、“表示学习”（与人工设计的特征不同）。