《机器学习》 第三章 线性模型

第三章 线性模型

3.1 基本形式

给定一个d维的描述示例的向量（特征）

$$\begin{align} \vec{x} = \left ( x_1; x_2; \cdots ; x_d \right ) \end{align}$$

线性模型试图通过学得一个通过属性的线性组合来进行预测的函数

$$\begin{align} f(x) &= w_1 x_1 + w_2x_2 + \cdots + w_d x_d + b \\ f(x)&= w^T x + b \end{align}$$

w和b学习得到之后，模型就确定了。

• 优点：

  1）简单、易于建模
  2）可引入层级结构或者高维映射使其变为更强大的非线性模型
  3）可解释性：最终的输出结果可以看作是不同属性的权重叠加

本章下文逻辑：
先从回归任务开始（线性），然后讨论二分类（对数几率回归、线性判别分析）和多分类任务。

3.2 线性回归

要解决的问题：

给定一个数据集D包含很多样本，每个样本包含多个属性，通过学习得到一个线性模型预测真实的输出标记。

离散属性如何表示？
1）若属性值之间存在“序”关系，可以通过连续化将其转化成为连续值。如高和矮可以量化为1和0。
2）若离散属性不存在“序”的关系，如果有k个属性值，通常转换成k维向量

3.2.1 一元线性回归分析

如何确定这个w和b呢？

均方误差通常是回归任务中常用的性能度量，因此我们可以让均方误差最小化，即

$$\begin{align} (w^*,b^*)&= \mathop{\arg \min} \limits_{(w,b)} \sum_{i=1}^{m}{(f(x_i)-y_i)^2} \\ &=\mathop{\arg\min}\limits_{(w,b)} \sum_{i=1}^{m}{(y_i-wx_i-b)^2} \end{align}$$

均方误差有很好的几何意义，对应了常用的欧氏距离，基于均方误差最小化来进行模型求解的方法称为“最小二乘法”，在线性回归中，最小二乘法就是找到一条直线，使得所有样本到直线上的欧氏距离最小。

求解的w和b过程就是使得上式最小化，求导即可：

$$\begin{align} \frac{\partial E_{(w,b)}}{\partial w} &= 2\left( w \sum_{i=1}^{m}{x_i^2} - \sum_{i=1}^{m}{(y_i - b)x_i}\right) \\ \frac{\partial E_{(w,b)}}{\partial w} &= 2\left( mb- \sum_{i=1}^{m}{(y_i - wx_i)} \right) \end{align}$$

到这一步是拆开平方项，求偏导即可

令上式等于0即可得到w和b的最优解的闭式解：

$$\begin{align} \hat{w} &= \frac{\sum_{i=1}^{m}{y_i(x_i-\bar x)}}{\sum_{i=1}^{m}{\left(x_i - \bar{x} \right) ^2} } \\ \hat{b} &= \bar{y} - \hat{\beta} \bar{x} \end{align}$$

上述公式推导在《数理统计》课程中也会有详细推导

3.2.2 多元线性回归分析

类似的，也可以用最小二乘法对w和b进行估计。为了方便讨论，会把w和b吸收成向量形式。

$$\begin{align} \hat{w} &= \{ w_1,w_2,…,w_d,b \} \\ \end{align}$$

样本特征增加一个维度，常量1，如下所示：

$$\begin{align} X &= \begin{pmatrix} x_{11} & x_{12} & … & x_{1d} & 1\\ x_{21} & x_{22} & … & x_{2d} & 1\\ \cdots & \cdots & \ddots & \cdots &\cdots \\ x_{m1} & x_{m2} & … & x_{md} & 1\\ \end{pmatrix} \end{align}$$

再把标签也写成向量形式，类似于w。有：

$$\begin{align} \hat{w}^* = \mathop{\arg \min} \limits_{\hat{w}} {(y-X \hat w)^T(y-X\hat w)} \end{align}$$

求偏导得：

$$\begin{align} \frac{\partial E_{\hat w}}{\partial \hat w} &= 2 X^T \left(X {\hat w} - y \right) \end{align}$$

由于涉及到矩阵逆的运算，会比较复杂。下面简单讨论：

1、如果 $X^TX$ 是满秩矩阵或正定矩阵 ，令上式为0，可得：

$$\begin{align} \hat{w}^* = (X^TX)^{-1}X^Ty \end{align}$$

这个式子也比较常见哦

2、往往不是可逆矩阵。比如变量超过样本数，不满秩，可以有多个解，均能使均方误差最小化。如何选择一个输出呢？常见的做法是引入正则化，约束w的大小。

3.2.3 扩展

线性回归模型虽然简单，但是可以有丰富的变化。

对于原始的模型，我们可以让模型的预测接近于y的衍生物。我们可以假设输出标记是在对数尺度上变化，那么就可以将对数作为线性模型的逼近的目标，即

这个特性很重要

$$\begin{align} \ln y = w^T x + b \end{align}$$

这就成为了“对数线性回归”，实际上让 $e^{w^Tx+b}$逼近于y。

更一般地，可以取单调可微函数g，使得：

$$\begin{align} y=g^{-1}(w^Tx+b) \end{align}$$

这样的模型称之为“广义线性模型”，函数g称为联系函数。

3.3 对数几率回归

上一节讨论的是回归，这一节讨论的则是分类。
答案蕴含在“广义线性模型中”：找一个单调可微函数，将线性回归的预测值与类别标记y联系起来。

考虑二分类任务输出为0,1，而回归任务的输出为实数值，所以需要将 实数值转换成 0/1。

理想的方法是单位阶跃函数，但是单位阶跃函数不连续，不能用。所以需要找一个近似的函数，即对数几率函数：

$$\begin{align} y= \frac{1}{1+e^{-z}} \end{align}$$

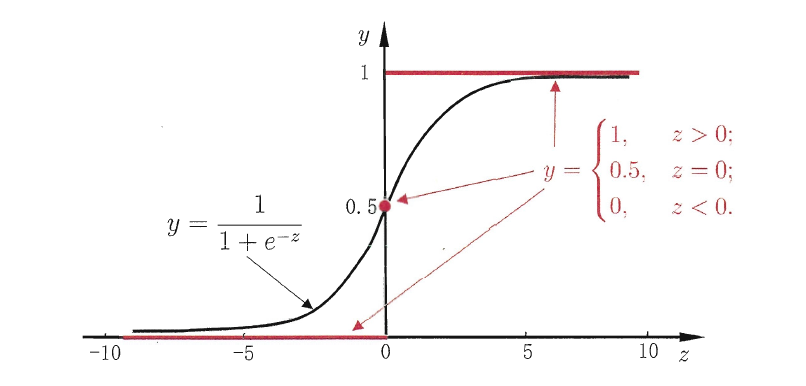
3.3.1 对数几率回归（logistics regression, logit regression）

对数几率是一种“Sigmod函数”，将z值转换成为0/1的y值。将z代入得到：

$$\begin{align} y= \frac{1}{1+e^{-(w^Tx+b)}} \end{align}$$

可以变化为：

$$\begin{align} \ln \frac{y}{1-y}=w^Tx+b \end{align}$$

将y看作是预测为正例的可能性，1-y为反例的可能性，那么两者的比值$\frac{y}{1-y}$称为“几率”，取对数$\ln \frac{y}{1-y}$，可以得到“对数几率”（称log odds, logit）。

因此，模型被称作是“对数几率回归”。虽然名字是回归，但是实际上是分类算法。

优点：
1）对分类可能性直接建模，无需事先假设数据分布。
2）不仅仅预测类别，还可以获得预测的可能性，对概论决策任务很有用。
3）目标函数任意阶可导的凸函数。

3.3.2 对数回归求解（略）

通过“最大似然法”估计参数，梯度下降法得到最优解

3.4 线性判别分析LDA

LDA的思想：
给定训练样本集合，将样本投影到一条直线上，使得同类样本尽可能近，不同类样本投影尽可能远；新样本来时，将其投影到同样的这条直线上，根据投影的位置来确定新样本的类别。

如下图所示：

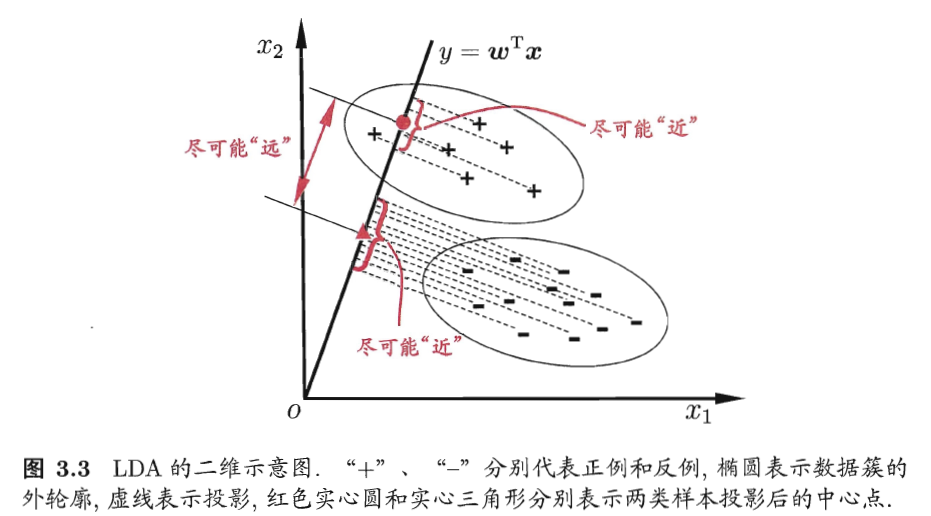
3.4.1 目标函数理论推导

给定数据集D，假设$X_i,\mu_i,\Sigma_i$分别为第i类的样本，均值向量、协方差矩阵。

将数据投影到直线$w$上，则两类样本的中心在直线上的投影为$w^T \mu_0和w^T \mu_1$；若将所有样本都投影到直线上，两类样本的协方差分别为$w^T \Sigma_0w和w_T \Sigma_1w$。

想要同类投影点尽可能近，可以让协方差尽可能小，即$w^T \Sigma_0w+w_T \Sigma_1w$尽可能小。不同类尽可能远离，可以让类中心距离尽可能大，即$\vert\vert w^T\mu_0-w^T\mu_1 \vert\vert_2^2$尽可能大。

同时考虑两者，那么目标为：

$$\begin{align} J &= \frac {\vert\vert w^T\mu_0-w^T\mu_1 \vert\vert_2^2} {w^T \Sigma_0w+w_T \Sigma_1w} \\ &= \frac {w^T (\mu_0-\mu_1)^T(\mu_0-\mu_1)w} {w^T (\Sigma_0+\Sigma_1)w} \end{align}$$

进一步化简：

定义：类内散度矩阵

$$\begin{align} S_w &= \Sigma_0+\Sigma_1 \\ &= \sum_{x \in X_0}{(x-\mu_1)(x-\mu_0)^T} + \sum_{x \in X_1}{(x-\mu_1)(x-\mu_1)^T} \end{align}$$

类间散度矩阵

$$\begin{align} S_b = (\mu_0-\mu_1)(\mu_0-\mu_1)^T \end{align}$$

则J可以重写为：

$$\begin{align} J &= \frac {w^T S_b w}{w^T S_w w} \end{align}$$

这就是LDA最大化的目标，广义瑞利商。

3.4.2 求解（略）

拉格朗日乘子法
最终结果为：

$$\begin{align} w=S_w^{-1}(\mu_0-\mu_1) \end{align}$$

3.5 多分类学习

有些二分类算法可以直接推广到多分类算法，但是更多情况下是基于这些基本策略，利用二分类学习器来解决多分类问题。

3.5.1 三种策略

1、一对一 OvO

将N个类别两两配对，产生N(N-1)/2个 分类器和结果，最终结果投票产生。

2、一对其余 OvR

一个类作为正例，其他类别作为反例，训练N个分类器。如果预测是仅有一个分类器预测为正例，那么就作为最终结果；如果有多个类，则根据置信度来判断。

对比：
OvO的存储开销和测试时间开销大，
OvR在训练时每个分类器均使用全部训练样例，因此训练时间开销大。

3、多对多 MvM

取若干类为正类，若干类为反类，但是要有独特的设计，不能随意选取。

介绍一种常用的技术：“纠错输出码”，ECOC

3.5.2 纠错输出码ECOC

• 编码：对N个类做M次划分，一部分作为正类，一部分作为反类，从而形成一个二分类训练集；这样有M个训练集和分类器
• 解码：对M个分类器分别进行测试，将测试结果组成一个编码。将这个预测编码和每个类别各自的编码进行比较，其中距离最小的作为最终结果。

常见的类别划分有二元码或三元码。三元码多了一个停用类。

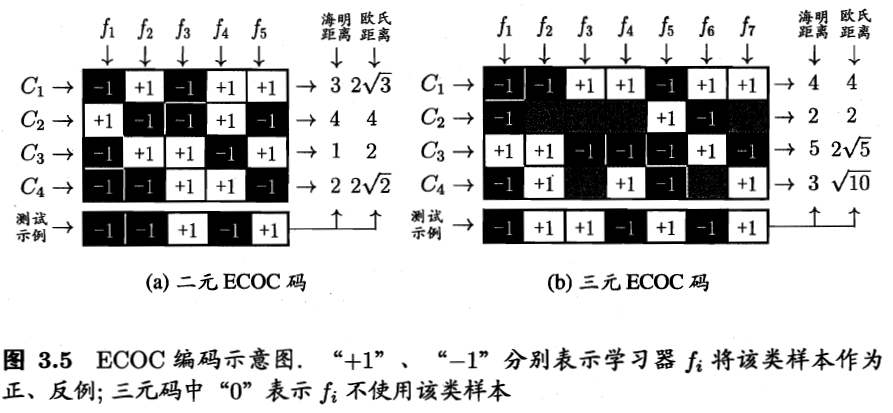
为什么称作是“纠错输出码”呢？
因为该编码对分类器的错误有一定的容忍和修正能力。某个结果错了，仍然可以得到正确的结果。

• 对于同一个任务，编码越长纠错能力越强；但是计算、存储开销也会增大；组合有限时，增长也会变得没有意义。
• 同等长度的编码，任意两个类别之间的距离越远，则纠错能力越强。但是当编码变长时，难以有效确定最优编码。

3.6 类别不平衡问题

前面的内容都有一个基本的假设，即不同类别的训练样本的数目基本相当。

类别不平衡是指：不同类别的训练样本数目差距很大的情况。

几率$\frac{y}{1-y}$反映了正例可能性和反例可能性的比值，阈值0.5表明分类器认为正反例可能性相同，因此当$\frac{y}{1-y}>1$时，预测为正例。

当正反例数目不同时，观测几率为：$\frac {m^+}{m^-}$，那么只要分类器预测几率高于观测几率即可判断为正例，即

$$\begin{align} \frac{y}{1-y}&>\frac{m^+}{m^-} \\ \frac{y'}{1-y'}&=\frac{y}{1-y}\times \frac{m^+}{m^-} \end{align}$$

这就是一个基本策略：“再缩放”（rescaling）

上述操作简单，但是实际操作不平凡。

现在的技术上大体分成三类：

• 1、对训练集里的负样本“欠采样”（undersampling）

欠采样时间开销小，代表性算法是：EasyEnsemble

• 2、对正样本“过采样”（oversampling）

不能简单重复采样，不然会严重过拟合。代表性算法是SMOTE：通过插值获得新样本。

• 3、在原训练集直接训练，预测过程中试用上述再缩放策略。