《深度学习》 章二 优化深度学习 第2节 优化算法

章二 优化深度学习 第2节 优化算法

第2节 优化算法

2.1 Mini-batch梯度下降法

深度学习（Deep Learning）就是更复杂的神经网络（Neural Network）

那么，什么是神经网络呢？下面我们将通过一个简单的例子来引入神经网络模型的概念。

建立房价的预测模型：

神经元

2.2 理解Mini-batch梯度下降法

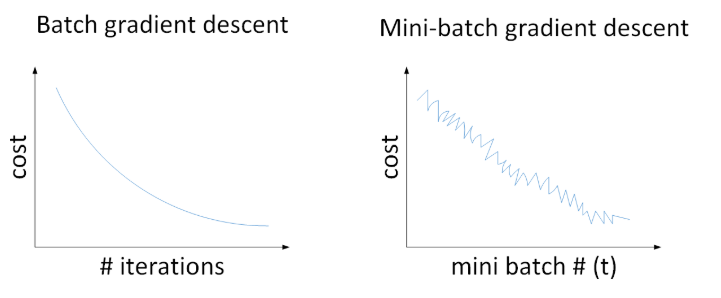
对于一般的神经网络模型，使用Batch gradient descent，随着迭代次数增加，cost是不断减小的。然而，使用Mini-batch gradient descent，随着在不同的mini-batch上迭代训练，其cost不是单调下降，而是出现振荡。但整体的趋势是下降的，最终也能得到较低的cost值。

之所以出现细微振荡的原因是不同的mini-batch之间是有差异的。

Batch gradient descent会比较平稳地接近全局最小值，但是因为使用了所有m个样本，每次前进的速度有些慢。随机梯度下降每次前进速度很快，但是路线曲折，有较大的振荡，不会收敛，最终会在最小值附近来回波动，难以真正达到最小值处。虽然可以通过降低学习率来减少噪声，但在数值处理上不能使用向量化的方法来提高运算速度。

2.3 指数加权平均

举个例子

记录半年内伦敦市的气温变化，并在二维平面上绘制出来，如下图所示：

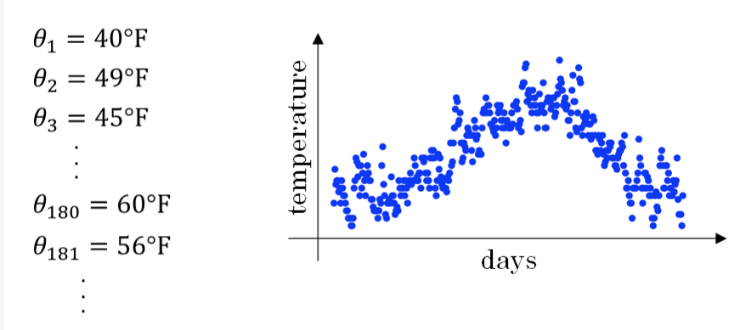
看上去，温度数据似乎有noise，而且抖动较大。如果我们希望看到半年内气温的整体变化趋势，可以通过移动平均（moving average）的方法来对每天气温进行平滑处理。

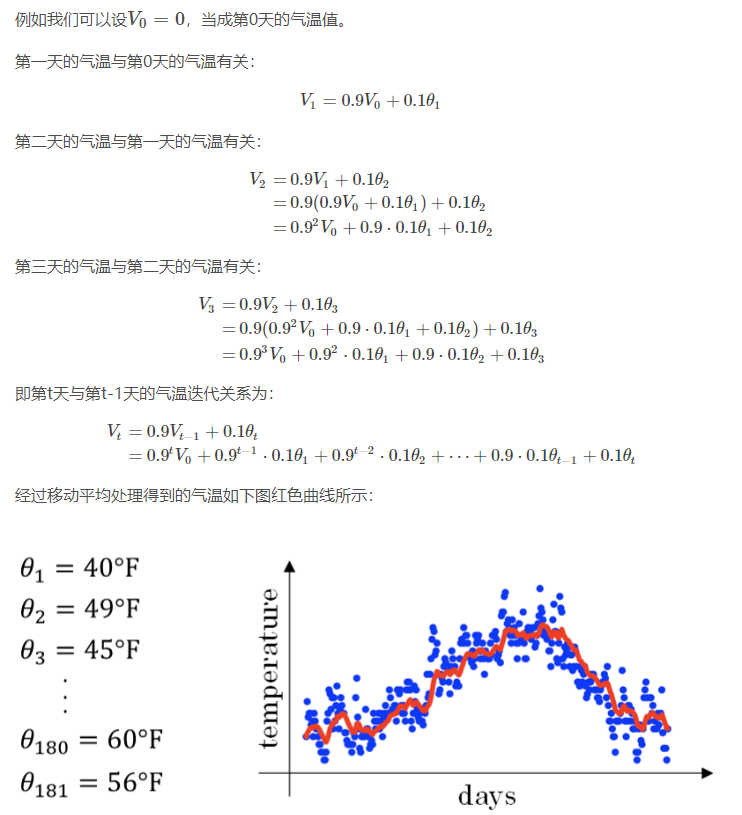
计算公式

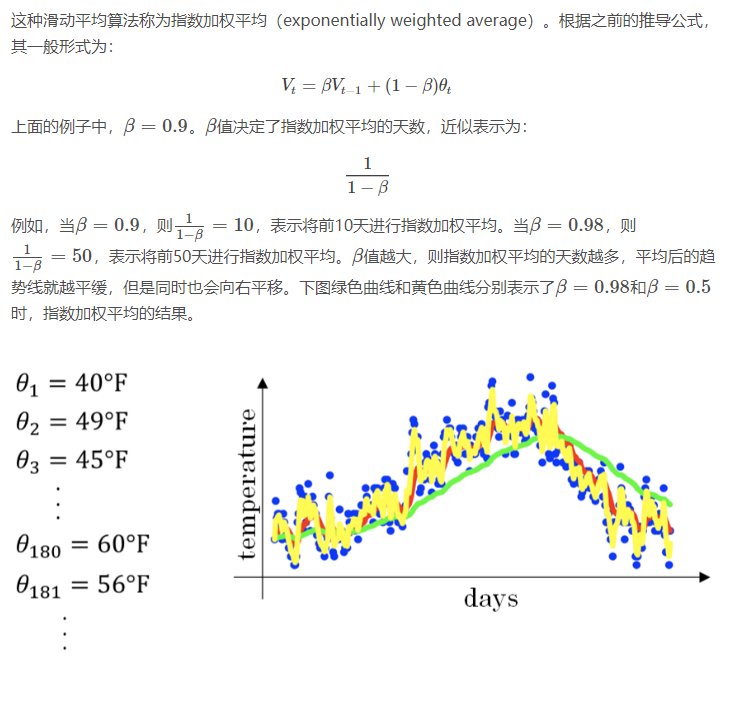
如何得到天数

2.4 理解指数加权平均

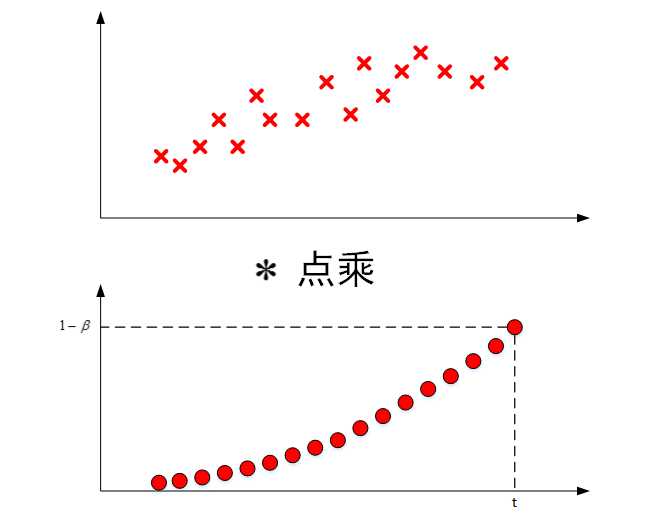
将原始数据值与衰减指数点乘，相当于做了指数衰减，离得越近，影响越大，离得越远，影响越小，衰减越厉害。

2.5 指数加权平均的修正

2.6 动量梯度下降法

动量梯度下降算法的速度要比传统的梯度下降算法快很多。

做法

是在每次训练时，对梯度进行指数加权平均处理，然后用得到的梯度值更新权重W和常数项b。

原始的梯度下降算法如上图蓝色折线所示。在梯度下降过程中，梯度下降的振荡较大，尤其对于W、b之间数值范围差别较大的情况。此时每一点处的梯度只与当前方向有关，产生类似折线的效果，前进缓慢。并且不能使用较大的学习率，否则会超出函数范围，只能选择较小的学习率。如果对梯度进行指数加权平均，这样使当前梯度不仅与当前方向有关，还与之前的方向有关，这样处理让梯度前进方向更加平滑，减少振荡，能够更快地到达最小值处。

2.7 RMSprop

RMSprop是另外一种加速梯度下降速度的算法。每次迭代训练过程中，其权重W和常数项b的更新表达式为：

也就是减小变得快的方向，加速变得慢的方向

2.8 Adam优化算法

前两种，一种是用指数加权平均的思想，另一种是除以一个系数，使得减小震荡。

Adam算法结合了动量梯度下降算法和RMSprop算法的优点，使得神经网络训练速度大大提高，且适用于多种网络结构。

其实也就是上面的三种思路结合起来，需要调试的也就是学习率

2.9 学习率衰减

减小学习因子能有效提高神经网络训练速度，这种方法被称为learning rate decay。

Learning rate decay就是随着迭代次数增加，学习因子逐渐减小。下图中，蓝色折线表示使用恒定的学习因子，由于每次训练相同，步进长度不变，在接近最优值处的振荡也大，在最优值附近较大范围内振荡，与最优值距离就比较远。绿色折线表示使用不断减小的，随着训练次数增加，逐渐减小，步进长度减小，使得能够在最优值处较小范围内微弱振荡，不断逼近最优值。相比较恒定的来说，learning rate decay更接近最优值

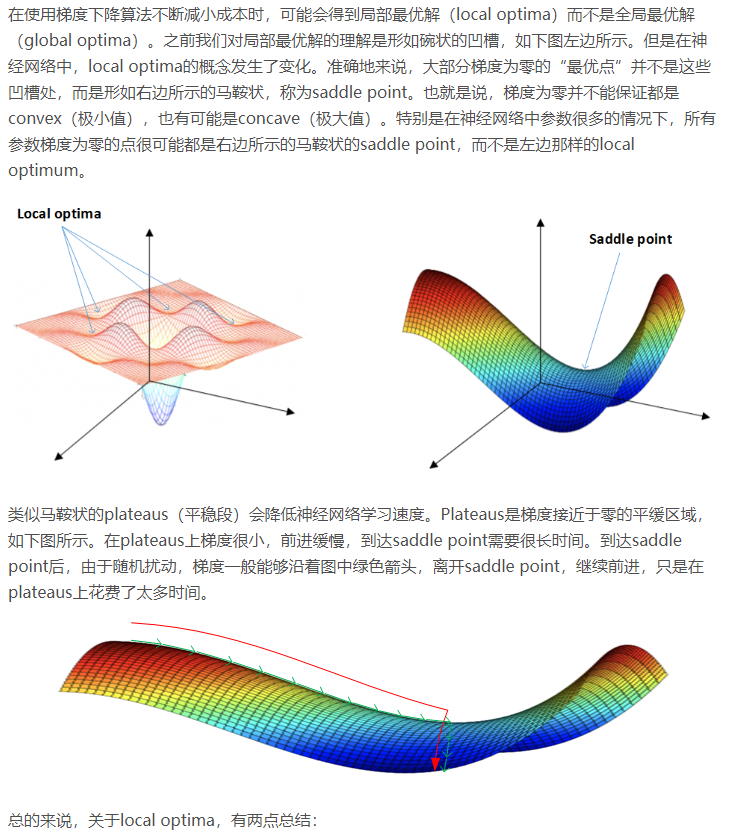
2.10 局部最优的问题

事实上，说是不太可能陷入极小值，好的优化算法都能有效解决下降慢的问题。