章一 神经网络与深度学习

第一节 深度学习概论

1.1 什么是神经网络

深度学习（Deep Learning）就是更复杂的神经网络（Neural Network）

那么，什么是神经网络呢？下面我们将通过一个简单的例子来引入神经网络模型的概念。

建立房价的预测模型：

神经元

一共有六个房子。我们已知输入x即每个房子的面积（多少尺或者多少平方米），还知道其对应的输出y即每个房子的价格。根据这些输入输出，我们要建立一个函数模型，来预测房价：y=f(x)。

我们会一条直线来拟合图中这些离散点，即建立房价与面积的线性模型。但是从实际考虑，我们知道价格永远不会是负数。所以，我们对该直线做一点点修正，让它变成折线的形状，当面积小于某个值时，价格始终为零。

几乎是一个最简单的神经网络。我们把该房价预测用一个最简单的神经网络模型来表示

Untitled

该神经网络的输入x是房屋面积，输出y是房屋价格，中间包含了一个神经元（neuron），即房价预测函数（蓝色折线）。该神经元的功能就是实现函数f(x)的功能。

上图神经元的预测函数（蓝色折线）在神经网络应用中比较常见。我们把这个函数称为ReLU函数，即线性整流函数（Rectified Linear Unit）

Untitled

上面讲的只是由单个神经元（输入x仅仅是房屋面积一个因素）组成的神经网络，而通常一个大型的神经网络往往由许多神经元组成，就像通过乐高积木搭建复杂物体（例如火车）一样。

神经网络

现在，我们把上面举的房价预测的例子变得复杂一些，而不是仅仅使用房屋面积一个判断因素。

例如，除了考虑房屋面积（size）之外，我们还考虑卧室数目（#bedrooms）。这两点实际上与家庭成员的个数（family size）有关。还有，房屋的邮政编码（zip code/postal code），代表了该房屋位置的交通便利性，是否需要步行还是开车？即决定了可步行性（walkability）。另外，还有可能邮政编码和地区财富水平（wealth）共同影响了房屋所在地区的学校质量（school quality）。

如下图所示，该神经网络共有三个神经元，分别代表了family size，walkability和school quality。每一个神经元都包含了一个ReLU函数（或者其它非线性函数）。那么，根据这个模型，我们可以根据房屋的面积和卧室个数来估计family size，根据邮政编码来估计walkability，根据邮政编码和财富水平来估计school quality。

最后，由family size，walkability和school quality等这些人们比较关心的因素来预测最终的房屋价格。

实际上，上面这个例子真正的神经网络模型结构如下所示。它有四个输入，分别是size，#bedrooms，zip code和wealth。在给定这四个输入后，神经网络所做的就是输出房屋的预测价格y。图中，三个神经元所在的位置称之为中间层或者隐藏层（x所在的称之为输入层，y所在的称之为输出层），每个神经元与所有的输入x都有关联（直线相连）。

Untitled

这就是基本的神经网络模型结构。在训练的过程中，只要有足够的输入x和输出y，就能训练出较好的神经网络模型，该模型在此类房价预测问题中，能够得到比较准确的结果。

1.2 使用神经网络进行监督学习

目前为止，由神经网络模型创造的价值基本上都是基于监督式学习（Supervised Learning）的。监督式学习与非监督式学习本质区别就是是否已知训练样本的输出y。

举例：

第一个例子还是房屋价格预测。根据训练样本的输入x和输出y，训练神经网络模型，预测房价。

第二个例子是线上广告，这是深度学习最广泛、最赚钱的应用之一。其中，输入x是广告和用户个人信息，输出y是用户是否对广告进行点击。神经网络模型经过训练，能够根据广告类型和用户信息对用户的点击行为进行预测，从而向用户提供用户自己可能感兴趣的广告。

第三个例子是电脑视觉（computer vision）。电脑视觉是近些年来越来越火的课题，而电脑视觉发展迅速的原因很大程度上是得益于深度学习。其中，输入x是图片像素值，输出是图片所属的不同类别。

第四个例子是语音识别（speech recognition）。深度学习可以将一段语音信号辨识为相应的文字信息。

第五个例子是智能翻译，例如通过神经网络输入英文，然后直接输出中文。

除此之外，第六个例子是自动驾驶。通过输入一张图片或者汽车雷达信息，神经网络通过训练来告诉你相应的路况信息并作出相应的决策。至此，神经网络配合监督式学习，其应用是非常广泛的。

Untitled

根据不同的问题和应用场合，应该使用不同类型的神经网络模型。

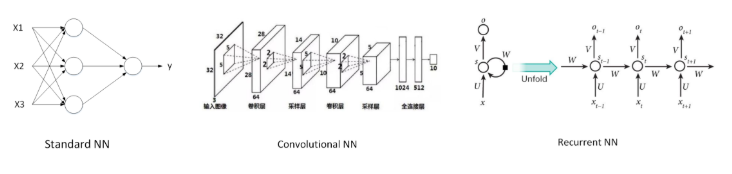
例如上面介绍的几个例子中，对于一般的监督式学习（房价预测和线上广告问题），我们只要使用标准的神经网络模型就可以了。而对于图像识别处理问题，我们则要使用卷积神经网络（Convolution Neural Network），即CNN。而对于处理类似语音这样的序列信号时，则要使用循环神经网络（Recurrent Neural Network），即RNN。还有其它的例如自动驾驶这样的复杂问题则需要更加复杂的混合神经网络模型。

CNN和RNN是比较常用的神经网络模型。下图给出了Standard NN，Convolutional NN和Recurrent NN的神经网络结构图。

Untitled

数据类型：

Structured Data和Unstructured Data。

Untitled

Structured Data通常指的是有实际意义的数据。例如房价预测中的size，#bedrooms，price等；例如在线广告中的User Age，Ad ID等。

而Unstructured Data通常指的是比较抽象的数据，例如Audio，Image或者Text。

总的来说，神经网络与深度学习无论对Structured Data还是Unstructured Data都能处理得越来越好，并逐渐创造出巨大的实用价值。

1.3 为什么深度学习这么强大

横坐标x表示数据量（Amount of data），纵坐标y表示机器学习模型的性能表现（Performance）

Untitled

传统机器学习算法在数据量较大的时候，性能一般，很难再有提升。然而，深度学习模型由于网络复杂，对大数据的处理和分析非常有效。

在处理海量数据和建立复杂准确的学习模型方面，深度学习有着非常不错的表现。然而，在数据量不大的时候，例如上图中左边区域，深度学习模型不一定优于传统机器学习算法，性能差异可能并不大。

强大的原因：三驾马车

  • Data

数据量的几何级数增加

  • Computation

加上GPU出现、计算机运算能力的大大提升，使得深度学习能够应用得更加广泛。

  • Algorithms

另外，算法上的创新和改进让深度学习的性能和速度也大大提升。

（举例：之前神经网络神经元的激活函数是Sigmoid函数，后来改成了ReLU函数。Sigmoid函数，在远离零点的位置，函数曲线非常平缓，其梯度趋于0，所以造成神经网络模型学习速度变得很慢。然而，ReLU函数在x大于零的区域，其梯度始终为1，尽管在x小于零的区域梯度为0，但是在实际应用中采用ReLU函数确实要比Sigmoid函数快很多。）

深度学习构建流程

首先产生Idea，然后将Idea转化为Code，最后进行Experiment。

接着根据结果修改Idea，继续这种Idea->Code->Experiment的循环，直到最终训练得到表现不错的深度学习网络模型。

如果计算速度越快，每一步骤耗时越少，那么上述循环越能高效进行。

第二节 神经网络基础之逻辑回归

2.1 二分类

逻辑回归模型一般用来解决二分类（Binary Classification）问题。

二分类就是输出y只有{0,1}两个离散值（也有{-1,1}的情况）。我们以一个图像识别问题为例，判断图片中是否有猫存在，0代表noncat，1代表cat。

通过这个例子简要介绍神经网络模型中一些标准化的、有效率的处理方法和notations。

notations：

cat图片的尺寸为（64，64，3）,将图片输入x（维度是（64，64，3））转化为一维的特征向量（feature vector）.。

方法是每个通道一行一行取，再连接起来。由于64x64x3=12288，则转化后的输入特征向量维度为（12288，1）。此特征向量x是列向量，维度一般记为nx。

如果训练样本共有m张图片，那么整个训练样本X组成了矩阵，维度是（nx，m）。

注意，这里矩阵X的行nx代表了每个样本x(i)特征个数，列m代表了样本个数。这里，Andrew解释了X的维度之所以是（nx，m）而不是（m，nx）的原因是为了之后矩阵运算的方便。

这里有一个注意的点：一列表示一个样本，行数是样本特征数

所有训练样本的输出Y也组成了一维的行向量，写成矩阵的形式后，它的维度就是（1，m）。

2.1 Logistic Regression

逻辑回归中，预测值h^=P(y=1 | x)表示为1的概率，取值范围在[0,1]之间。

使用线性模型，引入参数w和b。权重w的维度是（nx，1），b是一个常数项。

这样，逻辑回归的线性预测输出可以写成：y^=wTx+b

值得注意的是，很多其它机器学习资料中，可能把常数b当做w0处理，并引入x0=1。但在本课程中，为了简化计算和便于理解，建议使用上式这种形式将w和b分开比较好。

Sigmoid

上式的线性输出区间为整个实数范围，而逻辑回归要求输出范围在[0,1]之间，所以还需要对上式的线性函数输出进行处理。方法是引入Sigmoid函数，让输出限定在[0,1]之间。

y^=Sigmoid(wTx+b)=σ(wTx+b)

Untitled

还有一点值得注意的是，Sigmoid函数的一阶导数可以用其自身表示：

σ′(z)=σ(z)(1−σ(z))

2.3 逻辑回归的损失函数

逻辑回归中，w和b都是未知参数，需要反复训练优化得到。因此，我们需要定义一个cost function，包含了参数w和b。通过优化cost function，当cost function取值最小时，得到对应的w和b。

过去

平方错误（squared error）来衡量

Untitled

但

我们一般不使用平方错误来作为Loss function。原因是这种Loss function一般是non-convex的（非凸）。non-convex函数在使用梯度下降算法时，容易得到局部最小值（local minumum），即局部最优化。而我们最优化的目标是计算得到全局最优化（Global optimization）。因此，我们一般选择的Loss function应该是convex的。

交叉熵损失函数

Loss function的原则和目的就是要衡量预测输出y^与真实样本输出y的接近程度。平方错误其实也可以，只是它是non-convex的，不利于使用梯度下降算法来进行全局优化。

Untitled

Untitled

后面的课程中，我们将详细推导该Loss function是如何得到的。并不是凭空捏造的哦。。。

m个样本

Untitled

其实逻辑回归问题可以看成是一个简单的神经网络，只包含一个神经元。这也是我们这里先介绍逻辑回归的原因。

2.4 梯度下降

接下来将使用梯度下降（Gradient Descent）算法来计算出合适的w和b值，从而最小化m个训练样本的Cost function，即J(w,b)。

梯度下降算法是先随机选择一组参数w和b值，然后每次迭代的过程中分别沿着w和b的梯度（偏导数）的反方向前进一小步，不断修正w和b。每次迭代更新w和b后，都能让J(w,b)更接近全局最小值。梯度下降的过程如下图所示。

Untitled

Untitled

α是学习因子（learning rate），表示梯度下降的步进长度。α越大，w和b每次更新的“步伐”更大一些；α越小，w和b每次更新的“步伐”更小一些。

梯度下降算法能够保证每次迭代w和b都能向着J(w,b)全局最小化的方向进行。（如下图所示：）

Untitled

右边斜率会是正的，而左边会是负的。

2.5&6 导数、更多导数的例子（略）

2.7&8 计算图 、计算图的导数计算（略）

2.9 逻辑回归中的梯度下降

单个样本：

对单个样本而言，逻辑回归Loss function表达式如下

Untitled

该逻辑回归的正向传播过程非常简单。

Untitled

计算该逻辑回归的反向传播过程，即由Loss function计算参数w和b的偏导数。

Untitled

Untitled

m个样本上的梯度下降：

上一部分讲的是对单个样本求偏导和梯度下降。如果有m个样本，其Cost function表达式如下：

Untitled

1
2
3
4
5
6
7
8
9
10
11
12
13
J=0; dw1=0; dw2=0; db=0;
for i = 1 to m
    z(i) = wx(i)+b;
    a(i) = sigmoid(z(i));
    J += -[y(i)log(a(i))+(1-y(i)）log(1-a(i));
    dz(i) = a(i)-y(i);
    dw1 += x1(i)dz(i);
    dw2 += x2(i)dz(i);
    db += dz(i);
J /= m;
dw1 /= m;
dw2 /= m;
db /= m;

Untitled

第三节 Python与向量化

3.1 向量化

深度学习算法中，数据量很大，在程序中应该尽量减少使用loop循环语句，而可以使用向量运算来提高程序运行速度。

向量化（Vectorization）就是利用矩阵运算的思想，大大提高运算速度。

为了加快深度学习神经网络运算速度，可以使用比CPU运算能力更强大的GPU。事实上，GPU和CPU都有并行指令（parallelization instructions），称为Single Instruction Multiple Data（SIMD）。SIMD是单指令多数据流，能够复制多个操作数，并把它们打包在大型寄存器的一组指令集。SIMD能够大大提高程序运行速度，例如python的numpy库中的内建函数（built-in function）就是使用了SIMD指令。相比而言，GPU的SIMD要比CPU更强大一些。

3.2 向量化logistic回归及其梯度输出

逻辑回归：

利用向量化的思想，所有m个样本的线性输出Z可以用矩阵表示：

Untitled

在python的numpy库中可以表示为：

1
2
Z = np.dot(w.T,X) + b
A = sigmoid(Z)

梯度输出：

Untitled

db = 1/m*np.sum(dZ)

Untitled

dw = 1/m*np.dot(X,dZ.T)

这样，整个逻辑回归中的for循环尽可能用矩阵运算代替，对于单次迭代，梯度下降算法流程如下所示：

1
2
3
4
5
6
7
8
Z = np.dot(w.T,X) + b
A = sigmoid(Z)
dZ = A-Y
dw = 1/m*np.dot(X,dZ.T)
db = 1/m*np.sum(dZ)
 
w = w - alpha*dw
b = b - alpha*db

其中，alpha是学习因子，决定w和b的更新速度。上述代码只是对单次训练更新而言的，外层还需要一个for循环，表示迭代次数

3.3 Python中的广播

python中的广播机制可由下面四条表示：

  • 让所有输入数组都向其中shape最长的数组看齐，shape中不足的部分都通过在前面加1补齐
  • 输出数组的shape是输入数组shape的各个轴上的最大值
  • 如果输入数组的某个轴和输出数组的对应轴的长度相同或者其长度为1时，这个数组能够用来计算，否则出错
  • 当输入数组的某个轴的长度为1时，沿着此轴运算时都用此轴上的第一组值

Untitled

单个样本：

3.4 关于python/numpy向量的说明

python中，如果我们用下列语句来定义一个向量：

a = np.random.randn(5)

这条语句生成的a的维度是（5，）。它既不是行向量也不是列向量，它是rank 1 array。如果对a进行转置，会得到a本身。所以，如果要定义（5，1）的列向量或者（1，5）的行向量，最好使用下面的标准语句。

a = np.random.randn(5,1) b = np.random.randn(1,5)

还可以使用assert语句对向量或数组的维度进行判断：
assert(a.shape == (5,1))

assert会对内嵌语句进行判断，即判断a的维度是不是（5，1）的。如果不是，则程序在此处停止。使用assert语句是一种能够及时检查、判断语句是否正确的好习惯。
此外，还可以使用reshape函数对数组设定所需的维度：
a.reshape((5,1))

3.5 Explanation of logistic regression cost function(optional)

Untitled

注意问题：独立同分布和连乘

Untitled

第四节 浅层神经网络

4.1 神经网络概览

神经网络的结构与逻辑回归类似，只是神经网络的层数比逻辑回归多一层，多出来的中间那层称为隐藏层或中间层。从计算上来说，神经网络的正向传播和反向传播过程只是比逻辑回归多了一次重复的计算。正向传播过程分成两层，第一层是输入层到隐藏层，用上标[1]来表示；第二层是隐藏层到输出层，用上标[2]来表示。方括号上标[i]表示当前所处的层数；圆括号上标(i)表示第i个样本。

同样，反向传播过程也分成两层。第一层是输出层到隐藏层，第二层是隐藏层到输入层。

Untitled

4.2 神经网络表示

下面我们以图示的方式来介绍单隐藏层的神经网络结构。如下图所示，单隐藏层神经网络就是典型的浅层（shallow）神经网络。

Untitled

结构上，从左到右，可以分成三层：输入层（Input layer），隐藏层（Hidden layer）和输出层（Output layer）。输入层和输出层，顾名思义，对应着训练样本的输入和输出，很好理解。隐藏层是抽象的非线性的中间层，这也是其被命名为隐藏层的原因。

Untitled

最后，相应的输出层记为a[2]，即y^。

这种单隐藏层神经网络也被称为两层神经网络（2 layer NN）。之所以叫两层神经网络是因为，通常我们只会计算隐藏层输出和输出层的输出，输入层是不用计算的。这也是我们把输入层层数上标记为0的原因（a[0]）。

Untitled

4.3 计算神经网络的输出

计算输出：

Untitled

对于两层神经网络，从输入层到隐藏层对应一次逻辑回归运算；从隐藏层到输出层对应一次逻辑回归运算。每层计算时，要注意对应的上标和下标，一般我们记上标方括号表示第几层，下标表示第几个神经元。下标从1开始，上标从0开始。

从输入层到隐藏层的计算公式：

Untitled

从隐藏层到输出层的计算公式

Untitled

Untitled

上述每个节点的计算都对应着一次逻辑运算的过程，分别由计算z和a两部分组成。

为了提高程序运算速度，我们引入向量化和矩阵运算的思想，将上述表达式转换成矩阵运算的形式：

Untitled

矩阵维度：

Untitled

4.4 多个例子中的向量化

对于m个训练样本，我们也可以使用矩阵相乘的形式来提高计算效率。

对于每个样本i，可以使用for循环来求解其正向输出：

Untitled

不使用for循环，利用矩阵运算的思想，输入矩阵X的维度为（nx,m）。这样，我们可以把上面的for循环写成矩阵运算的形式：

Untitled

Untitled

维度理解：

行表示神经元个数，列表是样本数

4.5 激活函数

神经网络隐藏层和输出层都需要激活函数（activation function）。之前我们使用的是Sigmoid函数作为激活函数，下面是几个不同的激活函数：

sigmoid函数

Untitled

Untitled

Untitled

Untitled

如何选择合适的激活函数呢？

首先我们来比较sigmoid函数和tanh函数。对于隐藏层的激活函数，一般来说，tanh函数要比sigmoid函数表现更好一些。因为tanh函数的取值范围在[-1,+1]之间，隐藏层的输出被限定在[-1,+1]之间，可以看成是在0值附近分布，均值为0。这样从隐藏层到输出层，数据起到了归一化（均值为0）的效果。因此，隐藏层的激活函数，tanh比sigmoid更好一些。而对于输出层的激活函数，因为二分类问题的输出取值为{0,+1}，所以一般会选择sigmoid作为激活函数。

观察sigmoid函数和tanh函数，我们发现有这样一个问题，就是当|z|很大的时候，激活函数的斜率（梯度）很小。因此，在这个区域内，梯度下降算法会运行得比较慢。在实际应用中，应尽量避免使z落在这个区域，使|z|尽可能限定在零值附近，从而提高梯度下降算法运算速度。

为了弥补sigmoid函数和tanh函数的这个缺陷，就出现了ReLU激活函数。ReLU激活函数在z大于零时梯度始终为1；在z小于零时梯度始终为0；z等于零时的梯度可以当成1也可以当成0，实际应用中并不影响。对于隐藏层，选择ReLU作为激活函数能够保证z大于零时梯度始终为1，从而提高神经网络梯度下降算法运算速度。但当z小于零时，存在梯度为0的缺点，实际应用中，这个缺点影响不是很大。为了弥补这个缺点，出现了Leaky ReLU激活函数，能够保证z小于零是梯度不为0。

最后总结一下，如果是分类问题，输出层的激活函数一般会选择sigmoid函数。但是隐藏层的激活函数通常不会选择sigmoid函数，tanh函数的表现会比sigmoid函数好一些。实际应用中，通常会会选择使用ReLU或者Leaky ReLU函数，保证梯度下降速度不会太小。其实，具体选择哪个函数作为激活函数没有一个固定的准确的答案，应该要根据具体实际问题进行验证（validation）。

4.6 为什么需要非线性激活函数？

如果使用线性激活函数，最终得到的结果仍然是输入变量x的线性组合，即使用神经网络与直接使用线性模型的效果并没有什么两样。即便是包含多层隐藏层的神经网络，如果使用线性函数作为激活函数，最终的输出仍然是输入x的线性模型。这样的话神经网络就没有任何作用了。因此，隐藏层的激活函数必须要是非线性的。

但如果是预测问题而不是分类问题，输出y是连续的情况下，输出层的激活函数可以使用线性函数。如果输出y恒为正值，也可以使用ReLU激活函数，这里需要具体问题具体分析。

4.7 激活函数的导数

在梯度下降反向计算过程中少不了计算激活函数的导数即梯度。

Untitled

4.8 神经网络的梯度下降法

正向传播

Untitled

反向传播

Untitled

直观表示

对于单个训练样本

Untitled

总结一下，浅层神经网络（包含一个隐藏层），m个训练样本的正向传播过程和反向传播过程分别包含了6个表达式，其向量化矩阵形式如下图所示：

Untitled

4.9 随机初始化

神经网络模型中的参数权重W是不能全部初始化为零的，会导致隐藏层设置的多个神经元没有意义。但参数b可以初始化为0，并不会影响神经网络训练效果。

1
2
3
4
W_1 = np.random.randn((2,2))*0.01
b_1 = np.zero((2,1))
W_2 = np.random.randn((1,2))*0.01
b_2 = 0

乘以0.01的目的是希望初始化得到的W值尽量小，使用sigmoid函数或者tanh函数时能使z也比较小，提高梯度下降算法的运算速度。如果激活函数是ReLU或者Leaky ReLU函数，不需要考虑这个问题。但是，如果输出层是sigmoid函数，则对应的权重W最好初始化到比较小的值。

第五节 深层神经网络

5.1 深层神经网络

深层神经网络其实就是包含更多的隐藏层神经网络。下图分别列举了逻辑回归、1个隐藏层的神经网络、2个隐藏层的神经网络和5个隐藏层的神经网络它们的模型结构。

Untitled

命名规则上，一般只参考隐藏层个数和输出层。例如，上图中的逻辑回归又叫1 layer NN，1个隐藏层的神经网络叫做2 layer NN，2个隐藏层的神经网络叫做3 layer NN，以此类推。如果是L-layer NN，则包含了L-1个隐藏层，最后的L层是输出层。

标记写法

首先，总层数用L表示，L=4。输入层是第0层，输出层是第L层。

n[l]表示第l层包含的单元个数，l=0,1,⋯,L。这个模型中，n[0]=nx=3，

Untitled

5.2 深层网络中的前向传播

单个样本：

Untitled

m个样本

Untitled

Untitled

5.3 核对矩阵的维数

Untitled

n[l]和n[l−1]分别表示第l层和l−1层的所含单元个数。n[0]=nx，表示输入层特征数目。

Untitled

注意到，W[l]与dW[l]维度相同，b[l]与db[l]维度相同。这很容易理解。

Untitled

Untitled

5.4 为什么使用深层表示

更准确

多，神经网络就更加复杂和深入，学习也更加准确。

先来看人脸识别的例子，如下图所示。经过训练，神经网络第一层所做的事就是从原始图片中提取出人脸的轮廓与边缘，即边缘检测。这样每个神经元得到的是一些边缘信息。神经网络第二层所做的事情就是将前一层的边缘进行组合，组合成人脸一些局部特征，比如眼睛、鼻子、嘴巴等。再往后面，就将这些局部特征组合起来，融合成人脸的模样。可以看出，随着层数由浅到深，神经网络提取的特征也是从边缘到局部特征到整体，由简单到复杂。可见，如果隐藏层足够多，那么能够提取的特征就越丰富、越复杂，模型的准确率就会越高。

语音识别模型也是这个道理。浅层的神经元能够检测一些简单的音调，然后较深的神经元能够检测出基本的音素，更深的神经元就能够检测出单词信息。如果网络够深，还能对短语、句子进行检测。记住一点，神经网络从左到右，神经元提取的特征从简单到复杂。特征复杂度与神经网络层数成正相关。特征越来越复杂，功能也越来越强大。

减少神经元个数、减少计算量

Untitled

如果不用深层网络，仅仅使用单个隐藏层，那么需要的神经元个数将是指数级别那么大。

尽管深度学习有着非常显著的优势，Andrew还是建议对实际问题进行建模时，尽量先选择层数少的神经网络模型，这也符合奥卡姆剃刀定律（Occam’s Razor）。对于比较复杂的问题，再使用较深的神经网络模型。

5.5 搭建深层神经网络块

如下图所示，对于第l层来说，正向传播过程中：

Untitled

Untitled

Untitled

5.6 前向和反向传播

正向传播过程

Untitled

反向传播过程

Untitled

Untitled

5.7 参数VS超参数

该部分介绍神经网络中的参数（parameters）和超参数（hyper parameters）的概念。

神经网络中的参数就是我们熟悉的W[l]W[l]和b[l]b[l]。而超参数则是例如学习速率αα，训练迭代次数N，神经网络层数L，各层神经元个数n[l]n[l]，激活函数g(z)g(z)等。之所以叫做超参数的原因是它们决定了参数W[l]W[l]和b[l]b[l]的值。

如何设置最优的超参数是一个比较困难的、需要经验知识的问题。通常的做法是选择超参数一定范围内的值，分别代入神经网络进行训练，测试cost function随着迭代次数增加的变化，根据结果选择cost function最小时对应的超参数值。

5.8 这和大脑有什么关系?（略）